– Хорошо, допустим, что любой частоте можно сопоставить энергию и наоборот, – сказал Ассунто. – Твой светород заперт в некой потенциальной яме, и соответствующее ему волновое уравнение имеет два решения с определенными частотами.

– Да, – ответила Карла. – На рисунке я показала изменение двух волн в пространстве, однако сохраняя эту форму, они продолжают осциллировать во времени – каждая со своей собственной, единственной частотой.

– Затем ты добавляешь световую волну, частота которой совпадает с разностью частот светорода – и она постепенно подталкивает низкочастотную светородную волну в сторону более высоких частот?

– Именно.

– Ну что ж, в этом есть смысл, – сказал Ассунто. – Нечто подобное можно проделать с волнами в струне, если менять натяжение с частотой, равной разности между частотами двух резонансных мод.

– Но что более удивительно, – сказала Карла, – так это простое правило, которому подчиняется волна в процессе подобного перехода. Когда я изображала на графике доли каждой из волн, дуга, соединяющая точки, в которой суммарная волна совпадает соответственно с волной №1 и волной №2, не была каким-то художественным изыском: динамика действительно повторяет форму идеальной дуги окружности. На протяжении всего процесса сумма квадратов этих долей остается равной единице.

– Ясно. – Ассунто был готов поверить ей на слово, даже если значимость этой идеи обошла его стороной.

– Сосредоточьтесь на этой мысли, – сказала Карла.

Она достала второй лист бумаги.

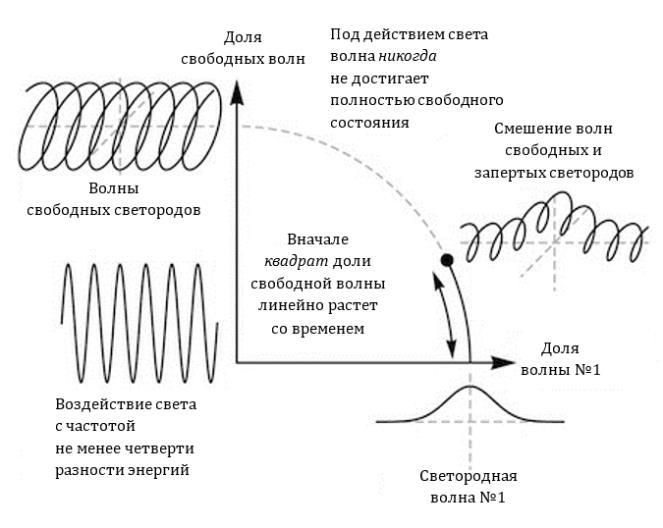
– Полагаю, это и есть плохая новость. – Ассунто изучил диаграмму. – Свет никогда не сможет освободить светород? Значит…, на твоей теории помутнения можно ставить крест?

– Погодите! – умоляюще возразила Карла. – Когда есть всего две волны, два уровня энергии, мы ожидаем, что динамика процесса превратит одну чистую волну в другую. В какую еще сторону ей двигаться? Но в данном случае существует целое множество свободных волн, частоты которых почти не отличаются друг от друга – и то, что я нарисовала на вертикальной оси включает в себя их все. А значит, в этом пространстве потенциальных возможностей можно бродить – поддерживая, как и раньше, сумму квадратов двух долей равной единице – не позволяя, доле запертой волны, падать до нуля.

– Не позволяя ей вообще сильно уменьшаться, – заметил Ассунто, указывая на скромный отрезок дуги, отображавший границы этого процесса. – Во что я охотно верю, с учетом твоих допущений. Но разве это не принципиальный изъян? Как это может быть описанием высвобождения светорода из потенциальной ямы под действием света, если волна практически не меняется независимо от длительности экспонирования?

Карла собралась с силами. В том, что ее гипотеза хоть сколько-нибудь тянет на вменяемую, ей удалось убедить Патрицию и Онесто, но настоящим испытанием станет Ассунто.

– Дело в том, – сказала она, – что мы не должны забывать о существовании других светородов и световых волн. Кроме того, есть целая пластина зеркалита. Мы можем представить большую часть ее воздействия в терминах простых «энергетических ям», но в реальности все обстоит сложнее. Если учесть, что светородные волны частично выходят за пределы своих ям, то каждый светород взаимодействует со своими соседями – а в какой-то степени и с соседями соседей, и так далее.

– Значит, твоя модель неадекватна? – предположил Ассунто.

– Да, – неохотно согласилась Карла. – Но модель всего твердого тела будет просто неподъемной. Единственный способ добиться хоть какого-то результата – это найти эмпирическое правило, которое позволит нам делать полезные прогнозы, исходя из того, что мы можем смоделировать.

Ассунто был настроен скептически.

– Какого рода правило?

– Для начала мы принимаем два вполне обоснованных допущения, – сказала Карла. – Если чистая волна, описывающая запертое состояние, взаимодействует со всем остальным твердым телом, она остается запертой. А если чистая волна, описывающая свободное состояние, взаимодействует с остальным твердым телом, то остается свободной.

– Это я могу пережить, – сказал Ассунто. – Но что произойдет со смесью двух волн?

– Я сомневаюсь, что мы вообще можем дать на этот счет какой-то надежный прогноз, – призналась Карла. – Если, во всяком случае, не знаем, как ведет себя каждый из светородов твердого тела. Но мы, вполне вероятно, можем предсказать поведение в среднем. Если считать, что квадрат доли запертой волны выражает вероятность того, что светород останется запертым в яме в результате взаимодействия с остальным твердым телом, то все обретает смысл – потому что квадраты долей в сумме дают единицу, точно так же, как равна единице сумма вероятностей для произвольного набора вариантов. Я знаю, это звучит слишком просто, чтобы быть правдой – но похоже, что в ситуации, когда мы не можем сделать точный прогноз, математика предлагает нам идеального кандидата на роль вероятности.

Ассунто поднял руку, прося тишины, и Карла дала ему время все обдумать.

– Когда именно эта вероятность обращается в действительность? – наконец, спросил он. – В твоем случае светородная волна меняет форму исключительно под влиянием света, но затем в какой-то момент она должна вступить во взаимодействие со всем остальным твердым телом, что, наконец-то и определит ее судьбу. Однако вероятность продолжает меняться по мере того, как меняет форму сама волна. Так какой именно вероятностью нужно пользоваться?

– Если взаимодействия происходят достаточно часто, а вероятность растет прямо пропорционально времени, конкретный момент не имеет никакого значения, – ответила Карла. – Предположим, что спустя одну паузу вероятность составляет один к гроссу, спустя две паузы – два к гроссу и так далее. Если все остальное твердое тело взаимодействует с каждым из светородов по одному разу за паузу, то скорость помутнения составит один светород на гросс в секунду. Но даже если взаимодействия происходят гораздо чаще, всякий раз, когда это случается, вероятность будет возрастать значительно слабее, чем в случае, если светород не вступал во взаимодействия более продолжительное время. Два эффекта – более низкая вероятность и большее число взаимодействий – практически полностью компенсируют друг друга, и в результате получается простая кривая экспоненциального затухания.

Она сделала набросок.

Ассунто это не впечатлило.

– Практически любой процесс выглядит линейным в достаточно малом масштабе, поэтому что бы ни происходило с патиной в действительности, конечный результат может оказаться похожим на экспоненциальное затухание. Если бы я выдал тебе солярит для очередного эксперимента, а ты бы вернулась ко мне вот с такой кривой, то что бы это доказало? Ничего.

– Одна кривая не несет никакого смысла, – согласилась Карла. – Но именно сейчас мы можем, наконец-то, реабилитировать плохую новость. Когда разница в уровнях энергии достаточно мала, чтобы с помощью света между двумя частотами можно было перебросить мост, скорость роста вероятности будет просто пропорциональна интенсивности света. Однако ряды, которые мы обнаружили в зеркалите, указывают на то, что разница между энергиями в четыре раза больше – а если речь идет о низкочастотном свете, то в пять. В этом случае скорость уже не будет пропорциональна яркости света – она будет пропорциональна ее четвертой или пятой степени.

Ассунто сразу же осознал значимость этого заявление.

– Стало быть, это эффект высшего порядка, – сказал он. – Световая волна вызывает в потенциальной яме малые возмущения, которые приводят к явлениям с некоторым нелинейным эффектом – а значит, полное описание процесса должно включать в себя все более мелкие слагаемые, зависящие от квадрата волны, ее куба, четвертой степени…